Вещественные числа

Перед тем как приступить к изучению форматов вещественных чисел, используемых сопроцессором, вспомним о числах с плавающей точкой, встречающихся в научных расчетах.

В общем виде эти числа можно записать следующим образом:

(знак)(мантисса)*10(знак)(порядок)

Например: -1.35*105.

Здесь знак - это минус, мантисса - 1.35, порядок - 5. Порядок тоже может иметь знак. В этом представлении чисел для вас вряд ли есть что либо новое. Вспомним также такое понятие, как норамализованное представление чисел:

• если целая часть мантиссы числа состоит из одной цифры, не равной нулю, то число с плавающей точкой называется нормализованным

В чем преимущества использования нормализованных чисел?

В том, что для фиксированной разрядной сетки числа (то есть для фиксированного количества цифр в числе) нормализованные числа имеют наибольшую точность. Кроме того, нормализованное представление исключает неоднозначность - каждое число с плавающей точкой может быть представлено различными (ненормализованными) способами:

123.5678*105 = 12.35678*106

= 1.235678*107 = 0.1235678*108

Для тех, кто программировал на языках высокого уровня, знакомо следующее представление чисел с плавающей точкой:

(знак)(мантисса)E(знак)(порядок)

Например, -5.35E-2 означает число -5.35*10-2. Такое представление называется научной нотацией.

Арифметический сопроцессор может работать с вещественными числами в трех форматах:

• одинарной точности;




• двойной точности;
• расширенной точности

Эти числа занимают в памяти, соответственно, 4, 8 или 10 байт (рис. 10.1).



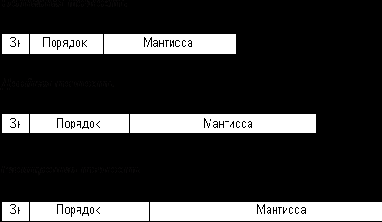
Рис. 10.1. Различные представления вещественных чисел

В любом представлении старший бит определяет знак вещественного числа:

• 0 - положительное число;
• 1 - отрицательное число

Все равные по абсолютному значению положительные и отрицательные числа отличаются только этим битом. В остальном числа с разным знаком полностью симметричны. Для представления отрицательных чисел здесь не используется дополнительный код, как это сделано в центральном процессоре.


Арифметический сопроцессор работает с нормализованными числами, поэтому поле мантиссы содержит мантиссу нормализованного числа.

Так как здесь используется двоичное представление чисел, сформулируем определение нормализованного числа для двоичного представления:


• если целая часть мантисса числа в двоичном представлении равна 1, то число с плавающей точкой называется нормализованным


Так как для нормализованного двоичного числа целая часть всегда равна единице, то эту единицу можно не хранить. Именно так и поступили разработчики арифметического сопроцессора - в форматах одинарной и двойной точности целая часть мантиссы не хранится. Таким образом экономится один бит памяти.

Для наглядности представим мантиссу числа в следующей форме:

n.nnnnnnnnnn...n

Здесь символом n обозначается либо 0, либо 1. Нормализованные числа в самой левой позиции содержат 1, поэтому их можно изобразить еще и в таком виде:

1.nnnnnnnnnn...n

Представление с расширенной точностью используется сопроцессором для выполнения всех операций. И даже более - все операции с числами сопроцессор выполняет над числами только в формате с расширенной точностью. В этом формате хранится и "лишний" бит целой части нормализованного числа.

Основная причина использования для вычислений расширенной точности - предохранение программы от возможной потери точности вычислений, связанной с большими различиями в порядках чисел, участвующих в арифметических операциях.

Поле порядка - это степень числа 2, на которую умножается мантисса, плюс смещение, равное 127 для одинарной точности, 1023 - для двойной точности и 16383 - для расширенной точности.

Для того, чтобы определить абсолютное значение числа с плавающей точкой, можно воспользоваться следующими формулами:

Одинарная точность:

1.(цифры мантиссы)*2(P-127)

Двойная точность:

1.(цифры мантиссы)*2(P-1023)

Расширенная точность:

1.(цифры мантиссы)*2(P-16383)

Знак числа, как мы уже говорили, определяется старшим битом.

Приведем конкретный пример. Пусть мы имеем число с одинарной точностью, которое в двоичном виде выглядит следующим образом:



1 01111110 11000000000000000000000

Для этого числа знаковый бит равен 1 (отрицательное число), порядок равен 126, мантисса - 11 (в двоичной системе счисления).

Значение этого числа равно:

1.11 * 2(126-127) = -1.75 * 2-1 = -0,875

Рассмотрим теперь особые случаи представления вещественных чисел.


• нуль - это такое число, у которого порядок и мантисса равны нулю. Нуль может иметь положительный или отрицательный знаки, которые игнорируются в операциях сравнения. Таким образом, имеется два нуля - положительный и отрицательный;



• наименьшее положительное число - это число, которое имеет нулевой знаковый бит, значение порядка, равное 1, и значение мантиссы, равное нулю. В зависимости от представления наименьшее положительное число имеет следующие значения: 1,17*10-38 (одинарная точность), 2.23*10-308
  
  (двойная точность), 3.37*10-4932 (расширенная точность);



• наибольшее отрицательное число - полностью совпадает с наименьшим положительным числом, но имеет бит знака, установленный в 1;



• наибольшее положительное число - это число, которое имеет нулевой знаковый бит, поле порядка, в котором все биты кроме самого младшего, равны 1, и содержит единицы во всех разрядах мантиссы. В зависимости от представления наибольшее положительное число имеет следующие значения: 3.37*1038
  
  (одинарная точность), 1.67*10308 (двойная точность), 1.2*104932
  
  (расширенная точность);



• наименьшее отрицательное число - полностью совпадает с наибольшим положительным числом, но имеет бит знака, установленный в 1;



• положительная и отрицательная бесконечность - это число содержит все единицы в поле порядка и все нули в поле мантиссы. В зависимости от состояния знакового бита может быть положительная и отрицательная бесконечности. Бесконечность может получиться, например, как результат деления конечного числа на нуль;



• нечисло - содержит все единицы в поле порядка и любое значение в поле мантиссы. Нечисло может возникнуть в результате выполнения неправильной операции при замаскированных особых случаях (ошибкам при работе с сопроцессоре будет посвящен отдельный раздел этой главы);



• неопределенность - содержит в поле порядка все единицы, а в поле мантиссы - число 1000..0 (для одинарной и двойной точности) или 11000..0 (для расширенной точности, так как в этом формате хранится старший бит мантиссы).


Для большей наглядности сведем все возможные представления вещественных чисел вместе на рис. 10.2.





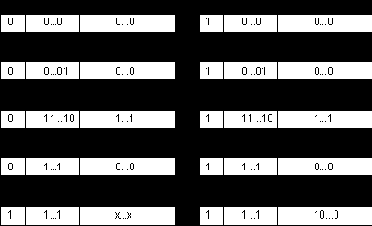
Рис. 10.2. Возможные предстваления вещественных чисел


Содержание раздела



---







---